When rendering a 3D game’s world, static meshes are often sufficient for modeling the environment like terrain, buildings and other objects. However, if we want it to appear inhabited, we won’t get around filling the world with creatures and characters that move and interact. This is where animation comes into play.

2D games typically realize such animations by displaying different sprite images in quick succession to create the illusion of motion. Composing a 3D animation of individual frames in a similar way, however, quickly becomes impractical due to the sheer amount of data. Instead, 3D games use an underlying bone structure to control a model’s movement in a technique called skeletal animation. This method is not only much more efficient than animating 3D models frame by frame, but also provides a more flexible workflow when animating and allows for perfectly smooth motion through interpolation.

With this article, I hope to provide an approachable introduction about the core concepts behind skeletal animation. We will explore what the skeleton structure actually is and how we can use it to move parts of our model. Since some parts of the process are simpler to understand by taking a look at an example, we will walk through the skeleton structure and animation of a simple robot model by Satendra Saraswat¹. By the end of this article you’ll be equipped with the fundamental principles that allow you to implement a skeletal animation system into your own game or game engine.

Prerequisites

Before getting started with skeletal animation, I recommend that you have a solid grasp of rendering static objects. This includes concepts like transforming vectors from one space to another using matrix transformations, vertex attributes and a good understanding of the render pipeline you’re using. If you’re using OpenGL, you should feel confident about vertex array objects with different vertex attributes and how to manipulate them using a vertex shader. LearnOpenGL is a great resource to get started.

The Skeleton

To make the robot move, we have to give it a skeleton. When creating a skeleton for a model (also called rigging), we have to think about how we want it to move later. The bones the skeleton consists of will be the units we will be able to move during the animating process. So, if we want the wrist of the character to move independently of the rest of the arm, we have to give it its own bone. This is what a skeleton for the robot may look like:

The skeleton in the picture above is in its default pose. Moving it into different poses should move the model’s vertices with it. To find out how we can make that happen, let’s start by looking at what bones actually are: Each bone \(b\) essentially consists of three properties:

• A list of child bones
• The offset transform \(\text{off}_b\)
• The parent transform \(\text{par}_b\)

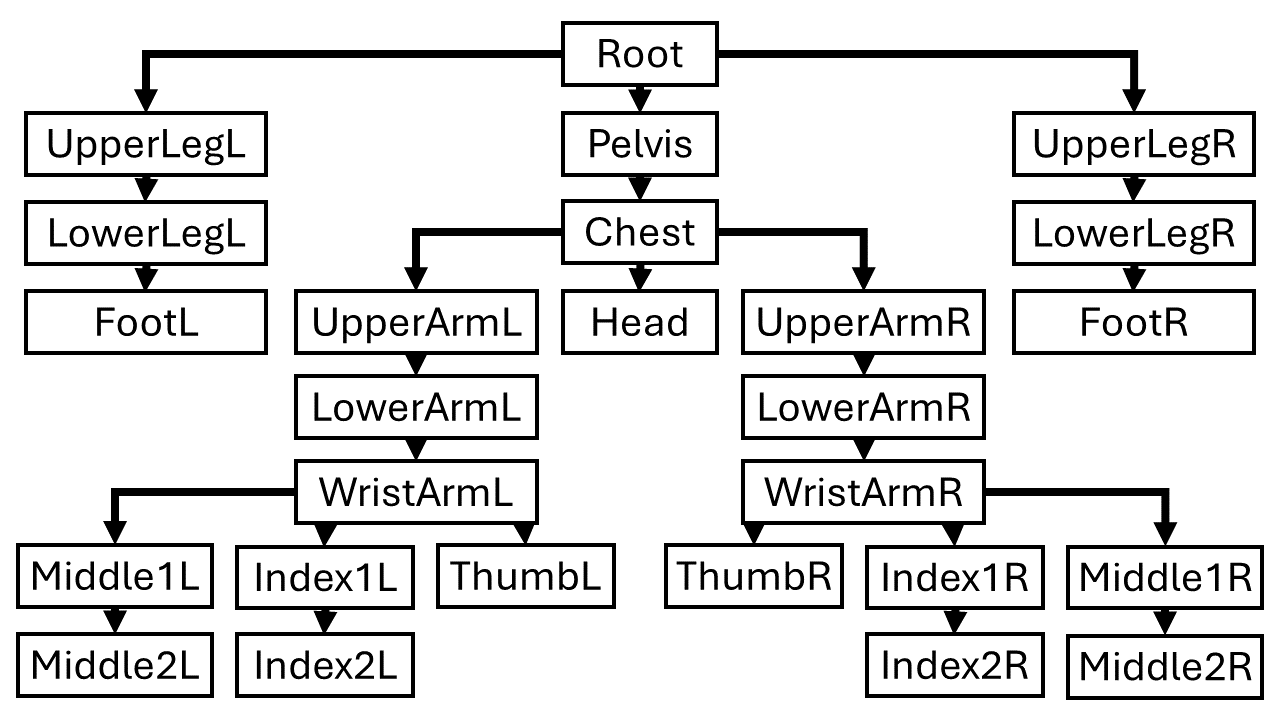
The bones in the skeleton compose a hierarchy with one common root bone. Moving one bone will affect all the bones below it in the hierarchy. Think about how we wouldn’t want the hand to stay in place when the robot moves its upper arm. To keep track of its place in the hierarchy, each bone holds a list of bones that come directly below it in the hierarchy - its children. The image below gives a schematic overview of the robot model’s bone hierarchy. Arrows point down the hierarchy, meaning each arrow coming from a bone in the image represents an entry in the bone’s list of children.

The other two properties are transforms, which we store as 4x4 matrices. The offset transform \(\text{off}_b\) describes the transformation from model to bone space, i.e. how we find the position of a vertex in relation to bone \(b\). This is independent of the skeleton’s pose, meaning the offset transform always describes the transformation from model to bone space while the bone is in its default pose. Since this means that the offset transform is constant, we don’t have to compute it ourselves but it is given to us as part of the output from modeling tools like Blender.

The parent transform \(\text{par}_b\) describes the transformation from the space of bone \(b\) to that of the parent bone. This is taking the skeleton’s pose into account so we will have to compute it ourselves depending on the bones’ relations to each other in the current pose of the skeleton. In the case of the root, which has no parent, the parent transform describes the transformation from root bone space back to model space. We will discuss how to compute parent transforms in the section Computing Parent Transforms. For now, let’s just assume we have already done that and know all the properties of each bone in the current pose.

Moving Vertices with the Skeleton

To make our model move, we need to transform its vertices to the correct position according to the current pose. The skeleton’s pose is fully defined by all the bones’ relations to their parents, which we store using the parent transforms.

The position attribute of each vertex is given in model space and represents vertex positions in the default pose. The first goal is to compute a transformation matrix for each bone \(b\), that maps a vertice’s model space position in the default pose to where it ends up in the current pose if it were fully dependent on \(b\)’s movement. In reality, vertices are often affected by multiple bones. At the end of this section, we will look at how to interpolate multiple bones’ effects on a vertex.

As an example, let’s work through the process for a vertex that moves with the chest bone of the skeleton: First, we need to compute the vertice’s position relative to the chest bone. The offset matrix of the chest bone \(\text{off}_\text{Chest}\) describes exactly this transformation from model- to bone space. From the vertice’s chest bone position, we work our way up through the hierarchy and take into account the relations between all bones along the way: The chest bone’s parent matrix \(\text{par}_\text{Chest}\) describes where a vertex in chest bone space would be as seen from pelvis bone space, taking into account the relation of chest and pelvis in the current pose. Thus, we get the correct position of the vertex in pelvis bone space. We repeat this process for each bone all the way up to the root. The root’s parent matrix \(\text{par}_\text{Root}\) describes the final step of transforming the vertex’s position in root space back to model space. You could think that we’re right back where we started, with the original vertex position in model space. However, since we went through all the relevant parent transforms on the way back up through the hierarchy, the new vertex position differs in that it follows the chest bone’s movement to where it is in the current pose. The final transformation of the original vertex position \(v_\text{orig}\) to its animated position \(v_\text{anim}\) can be written like this:

\(v_\text{anim} = \text{par}_\text{Root} \cdot \text{par}_\text{Pelvis} \cdot \text{par}_\text{Chest} \cdot \text{off}_\text{Chest} \cdot v_\text{orig}\)

Let’s call the product of the parent and offset matrices \(\text{final}_\text{Chest} = \text{par}_\text{Root} \cdot \text{par}_\text{Pelvis} \cdot \text{par}_\text{Chest} \cdot \text{off}_\text{Chest}\), or more generally \(\text{final}_b\) for any bone \(b\). We don’t want to compute this transformation on the fly for every vertex. Instead, we can write a recursive function to traverse the bone hierarchy and compute each bone’s final transformation matrix every time the pose changes (which is typically every frame). In pseudo-code, such a function could look like this:

void ComputeFinalTransforms(Bone b, Matrix4 parentToModelSpace,
                            Matrix4[] finalMatrices){
    
    // Compute bone b's final transform matrix
    Matrix4 selfToModelSpace = parentToModelSpace * b.parentTransform;
    finalMatrices[b.ID] = selfToModelSpace * b.offsetTransform;

    // Recursively traverse the bone hierarchy
    foreach (Bone child : b.children){
        ComputeFinalTransforms(child, selfToModelSpace, finalMatrices);
    }
}

To start the hierarchy traversal, we call this function for the root node:

Matrix4 finalMatrices[nBones];
ComputeFinalTransforms(root, Matrix4.Identity, finalMatrices);

To store the final transforms, we can assign each bone a unique integer ID ranging from \(0\) to \(n-1\), where \(n\) is the number of bones in the hierarchy. We use that ID to access an array of matrices which we use to store all final transform matrices. We will see how that comes in handy in the next step.

Now that we computed our final transform matrices, describing for each bone how a vertex should be transformed to follow that bone’s movement in the current pose of the skeleton, we still need to actually use them to transform the model vertices. For this, we need to know what bones each vertex is influenced by. Note that a vertex might be influenced by multiple bones, e.g. vertices near a joint. This is typically part of the output from modeling and animation tools like Blender. We want to save this information as vertex data. So, apart from vertex position (and other vertex data like uv-coordinates or normals), we save two additional vectors per vertex:

• A Vector of bone IDs the vertex is influenced by and
• A Vector of weights corresponding to the impact each bone reffered to by the ID vector has on the vertex.

Keeping these as 4-dimensional vectors (i.e. limiting the number of bones that influence each vertex to 4) is typically enough. This way, weights.x denotes the percentage with which the bone with ID boneIDs.x influences the vertex and analogously for y, z and w components. It is important to make sure that the entries in the weight vector add up to 1. Finally, we need to transform vertex positions with each of the influencing bones and interpolate the result according to the given weights. With OpenGL, this would happen in a vertex shader and could look like this:

#define MAX_BONES 128

// Vertex Attributes
layout (location = 0) in vec3 aPosition;
layout (location = 1) in vec2 aTexcoord;
layout (location = 2) in vec4 aBoneId;
layout (location = 3) in vec4 aWeight;

// Outputs to fragment shader
out vec2 vTexcoord;

// ModelViewProjection Matrix
uniform mat4 mvp;

// Array of final bone matrices
layout(std140) uniform FinalBoneMatrices {
    mat4 finalBoneMatrices[MAX_BONES];
};

void main()
{
    vTexcoord = aTexcoord;

    // Transform vertex with each influencing bone
    //  and interpolate result using weights.
    vec4 animatedPos = (aWeight.x * finalBoneMatrices[int(aBoneId.x)] + 
                        aWeight.y * finalBoneMatrices[int(aBoneId.y)] + 
                        aWeight.z * finalBoneMatrices[int(aBoneId.z)] + 
                        aWeight.w * finalBoneMatrices[int(aBoneId.w)]) * vec4(aPosition, 1.0);

    gl_Position = mvp * animatedPos;
}

If your model contains vertex normals, you can transform them the same way. Note though that if your animation contains non-uniform scaling, normals need to be transformed using the transposed inverse of the final bone matrices.

Computing Parent Transforms

We now know how the bones are structured hierarchically to form a skeleton and how we use this structure to transform vertices to move with the bones, assuming the bones are fully defined with an offset and parent transform. The last missing piece to the puzzle is to define the pose of the skeleton at each frame during the animation. Recall that we store a pose using the bones’ parent transform matrices. So it is these matrices that we need to compute.

Let’s first take a look at how animations are stored: Animation tools like Blender structure them in keyframes. A keyframe \(k\) for a bone \(b\) consists of two parts:

• A timestamp \(t_k\) defining at what time during the animation this keyframe defines the pose of bone \(b\)
• The relation of bone \(b\) to its parent, namely a translation vector, a rotation quaternion and a scaling vector.

The translation vector describes how far away and in what direction the origin of bone \(b\)'s space is as seen from the parent's origin. The rotation quaternion describes how bone \(b\)'s space is rotated as seen from the parent bone. Quaternions might seem daunting and unintuitive when you first encounter them. Luckily, we don't need a very deep understanding of them to animate the skeleton. I recommend 3Blue1Brown's explanation if you're interested anyway. Essentially, quaternions are a neat way to represent rotation in 3D space. We use them, because they allow us to interpolate between two rotations. Naively interpolating rotation angles around each axis leads to a phenomenon called gimbal lock, which we can avoid using quaternions. For our purpose, we only need to interpolate between quaternions and convert them to a rotation matrix, which are functions that many maths libraries implement for us. Lastly, the scaling vector describes the scale of bone \(b\)'s space relative to that of the parent bone. Usually, when animating characters, we don't deal with scaling a lot. Though, it's good to know that the possibility exists.

Keyframes describe the pose of the skeleton at exactly the time noted in their timestamp. To find the pose of the skeleton between two keyframes, we have to blend the poses of the previous and the next keyframe. The most straight forward way to do this is using linear interpolation. The image below shows what an animation timeline with 3 keyframes could look like:

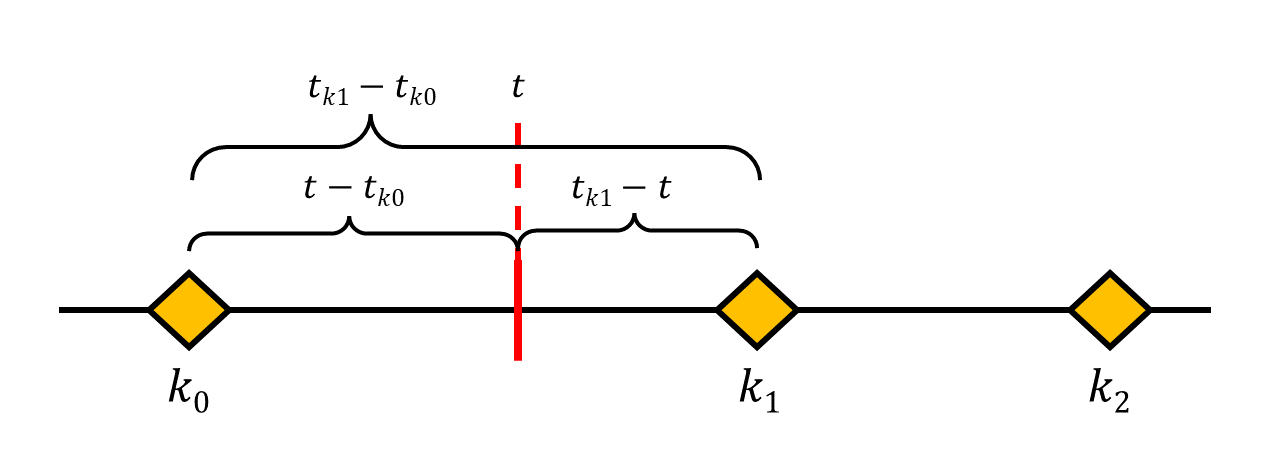
To find the skeleton’s pose at time \(t\), we need to interpolate between keyframes \(k_0\) and \(k_1\). The image also shows the time intervals between \(t\) and the key frames that we can use to determine how close the blended pose should be to either of the keyframes. As \(t\) gets closer to \(k_1\), \(\frac{t-t_{k0}}{t_{k1}-t_{k0}}\) will approach \(1\), while \(\frac{t_{k1} - t}{t_{k1}-t_{k0}}\) approaches \(0\). So using \(w_0 = \frac{t_{k1} - t}{t_{k1}-t_{k0}}\) and \(w_1 = \frac{t-t_{k0}}{t_{k1}-t_{k0}}\) as interpolation weights will give us a smooth blending between the keyframes.

Interpolating translation and scaling vectors is quite straight forward: \(\text{translation}_\text{blended} = w_0 \cdot \text{translation}_{k0} + w_1 \cdot \text{translation}_{k1}\) \(\text{scaling}_\text{blended} = w_0 \cdot \text{scaling}_{k0} + w_1 \cdot \text{scaling}_{k1}\)

Blending rotation quaternions is a little more involved. We use a method called spherical linear interpolation (SLerp). Luckily, most libraries that implement Quaternions do the heavy lifting for us.

Now that we have the interpolated translation, rotation and scaling components, we can finally use them to construct the parent matrix. Remember, that the parent matrix describes the transformation from bone \(b\) to its parent. It might be necessary to invert it, depeding on how translation, rotation and scaling are stored.

Conclusion

This covers the basics of skeletal animation, from the skeleton’s structure and how it’s animated to how we make the vertices move with it. This is of course far from all you can do about animating models. Interesting ideas to continue with might include:

• Blend Trees to blend between animations
• Inverse Kinematics to automatically adjust the skeleton's pose based on the desired position of a hand or foot
• Procedural Animation